1. Введение. Основные понятия.
2. Логические функции.
3. Построение логических выражений.
4. Основные законы логики.
5. Преобразование и упрощение логических выражений.
6. Решение логических задач.
7. Основы компьютерной микросхематики.
Введение. Основные понятия.
В начало
Логика – наука о формах и способах рассуждений.
Зачем необходимо знать ее основы?
Зная законы физики, вы прекрасно представляете, что с метровой высоты прыгать можно, а с
десятиметровой опасно. Зная логические законы, вы сможете, совершенно однозначно,
определять: произойдет то или иное событие при наличии определенных условий или
нет, а не действовать наугад.
Когда мы бросаем камень, он летит, подчиняясь законам физики, когда мы солим
пищу, соль растворяется, подчиняясь законам химии, когда
мы рассуждаем или
просто общаемся, не замечая этого, мы подчиняем свои рассуждения законам логики.
Когда мы говорим, это правда, а это ложь, или, если получится, это и это, то
будет то, или это никогда не произойдет без этого – мы выстраиваем суждения по
законам логики.
Формальная логика отделяет содержание процесса мышления от его общих принципов.
Это означает, например, если вы обещаете прибыть на встречу, то
для логики важно
прибудете или нет, а на каком виде транспорта и в какой одежде для нее не имеет
значения.
Или, когда вы говорите: я выпью кофе, если он будет крепким, сладким и горячим,
для логики не имеет значения, кто, как, когда и каким способом будет готовить
условия для логичного завершения действия.
Логика изучает структуру процесса мышления. Мышление это сложный процесс, но и
его можно разложить на некоторое количество форм (то, при помощи чего мы
выражаем свои мысли), которые объединяются по общим признакам.
Итак, мышление может быть
выражено следующими формами.
1. Понятие
2. Суждение (высказывание).
3. Умозаключение
4. Доказательство.
Понятие – форма мышления, отражающая существенные формы предмета или явления. (Яркий
свет, круглый камень, холодная погода).
Высказывание это форма мышления, выраженная при помощи понятий, когда что-то
утверждается или отрицается.
- Половины бака бензина недостаточно, чтобы доехать до места.
- Монета упала изображением номинала (решкой) вверх.
- Спортсмен преодолел планку на высоте 2.20.
- Из-за обрыва провода не воспроизводится звук в наушниках MP3 плейера.
- Я еду с требуемой скоростью при виде знака по ее ограничению.
Высказывание существует в двух формах – ИСТИНА и ЛОЖЬ
Суждение истинно, если оно правильно отражает свойства или отношения реальных
вещей.
Суждение ложно, если оно искажает объективные отношения.
Фундаментальное понятие логики – она не рассматривает обоснование истинности.
В естественном языке высказывание – повествовательное предложение. Высказывания
используют формальные языки – математика, физика, химия. Электронные устройства,
в том числе и компьютерные тоже могут обмениваться высказываниями (сообщениями),
которые, тоже могут подчиняться законам логики.
Высказывание считается простым, если никакая из его частей не является
высказыванием.
Логические функции.
В начало
Основная задача - логики рассмотрение сложных логических выражений.
Простые высказывания соединяются в сложные
при помощи логических связок (функций).
Логическая функция это формальное правило преобразования или объединения
высказываний, пришедшее в логику из обычной жизни.
Основные логические функции:
Инверсия – НЕ
Функция преобразующая исходное высказывание в обратное.
- Приятель будет звонить мне в 17.00. (А он не позвонил)
- Кран сможет поднять груз на эту высоту. (А он не смог)
- Прошел дождь - полив не требуется
Дизъюнкция – ИЛИ логическое сложение.
- Ты должен помыть посуду или убраться в комноте, тогда пойдешь гулять. (Необходимо
выполнить или то, или то, в этом случае результатом будет истина и вы пойдете
гулять)
Конъюнкция – И логическое умножение.
- Вы должны владеть иностранным языком и иметь высшее образование, только тогда
вас возьмут на работу. (Наличие одного из условий не обеспечивает вашего приема
на работу. Только в случае если и первое и второе выполняется тогда результатом
станет истина - прием на работу)
Импликация – следование.
(Импликация не имеет простой жизненной интерпретации). Для себя я ее определяю
по следующему правилу. Трагедия в том, что хотел, но не получилось.
В результате: Хотел и получилось - это истина. Не хотел, а получилось, тоже
истина. Не хотел и не получилось истина потому, что мне нет до этого никакого
дела.
Эквиваленция – равенство. Здесь все просто - результат - истина если исходные
высказывания эквивалентны: оба истины или ложны.
Договоримся обозначать простые высказывания заглавными буквами английского
алфавита.
И сведем обозначения логических связок в таблицу
Таблица обозначений логических связок - функций
| Логическая связка (функция) | Обозначение | Название |
| A и B | A & B, A and B, A Λ B | Конъюнкция |
| A или B | A V B, A or B | Дизъюнкция |
| Не А , A неверно |
_ ¬ A, A |
Инверсия |
| Из A
следует B, Если A то B, A влечет B, B следствие A |
A -> B, If A then B | Импликация Следование |
| A равно B | A <--> B | Эквиваленция |
Результирующее
высказывание, полученное из простых путем их объединения при помощи
логической функции может быть, как истинным так и
ложным. Для каждой из функций объединение
происходит по определенным правилам. Необходимо рассматривать
все случаи исходных высказываний. Правила
объединения исходных высказываний принято сводить в
таблицы. Такие таблицы называются таблицами
истинности.
Принято ложь определять как 0, а истину, как 1.
Таблицы истинности для логических функций.
Конъюнкция. И &
| A | B | C |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Дизъюнкция. ИЛИ V
| A | B | C |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Инверсия. НЕ
| A | B |
| 0 | 1 |
| 1 | 0 |
Импликация. ->
| A | B | C |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
Эквиваленция. <-->
| A | B | C |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Построение (запись) логических выражений.
В начало
Каждое сложное (составное) высказывание можно выразить в виде формулы – логического выражения.
В выражение входят:
- логические переменные,
которые обозначают высказывания
- знаки логических операций, которые обозначают логические функции.
Для составления выражений на языке алгебры логики нужно выделить простые высказывания и логические связки между ними.
Рассмотрим пример логического выражения.
(X * Y = 5 или X * Y = 4 ) И (X * Y ≠ 5 или X * Y ≠ 4)
Подставим в выражение значения x=2, y=2
(2 * 2 = 5 или 2 * 2 = 4) И (2 * 2 ≠ 5 или 2 * 2 ≠ 4)
Выделяем простые высказывания и связки
( A или B ) И (¬A или ¬B )
Запишем выражение логической функции
F = ( A V B ) & (¬A V ¬B )
Подставим в функцию формальные значения высказываний.
F = ( 0 V 1) & (1 V 0) = 1 & 1 = 1 - для данных условий результирующим значением функции является истина
Для выяснения поведений функций в любых ситуациях строят для них таблицы истинности.
Количество проверяемых комбинаций равно 2n
- где n – количество логических переменных.
Рассмотрим следующую функцию: F = ( A V B ) & (¬A V ¬B )
| А | B | A V B | ¬A | ¬B | ¬A V ¬B | F |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Хотя логика работает с формальными логическими выражениями, всегда подразумевается, что эти выражения запись жизненной ситуации, математической задачи, режимов работы электронных или компьютерных устройств и так далее.
Рассмотрим несколько примеров построения
логических выражений.
Пример 1.
Постановка условия:
Если придет Вася или Коля и мама разрешит, то пойду
гулять.
Обозначим :
| Приход Васи | A | |
| Приход Коли | B | |
| Разрешение мамы | C |
Запишем логическую функцию F = ( A V B )
& C
Составим таблицу истинности
| A | B | A V B | C | ( A V B ) & C |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 |
Создание таблицы истинности позволяет
рассмотреть все возможные ситуации и получить для каждого случая результирующее
значение логического выражения.
Пример 2
Постановка условия:
Выбрать из массива нечетные положительные числа
Четное число A
Нечетное число ¬A
Положительное число B
| Четное число | A | |
| Нечетное число | ¬A | |
| Положительное число | B |
F = ¬A & B
Таблица истинности
| A |
¬A |
B | ¬A & B |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
Пример 3
Постановка условия: Имеем массив
из N целых положительных чисел. Подсчитайте количество четных и нечетных.
Если X – четное
A
Если X – нечетное ¬A
Логическая функция F = A V ¬A
| A | ¬A |
A V ¬A |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
И что же мы имеем?
A V ¬A = 1
Дизъюнкция высказывания с инверсией всегда истинна.
И вправду, какими же еще могут быть целые положительные
числа?
Основные законы логики.
В начало
Логические выражения могут быть равносильно преобразованы из одной формы в
другую согласно законам логики. Рассмотрим кратко основные из них.
1. Двойного отрицания:
А = ¬(¬A)
2. Переместительный (коммутативный) :
A V B = B V A
A & B = B & A
3. Сочетательный (ассоциативный):
(A V B) V C = A V (B V C)
(A&B) & C = A & (B & C)
4. Распределительный (дистрибутивный)
(A V B) & C = (A & C) V (B & C)
(A & B) V C = (A V C) & (B V C)
5. Закон общ. инверсии (законы де Моргана):
¬( A V B) = ¬A & ¬B
¬(A & B) = ¬A V ¬B
A à B = ¬A V B
¬(A à B) = A & ¬B
6. Закон идемпотентности
A V A = A
A & A = A
7. Законы исключения констант:
A V 1 = 1, A V 0 = A
A & 1 = A, A & 0 = 0
8.
Закон противоречия:
A & ¬A= 0.
9. Закон исключения третьего:
A V ¬A = 1.
10. Закон поглощения:
A V (A & B) = A;
A & (A V B) = A.
11. Закон исключения (склеивания):
(A&B) V (¬A & B) = B
(A V B) & (¬A V
B) = B
Я не задерживался здесь
подробно потому, что
основные законы
логики стройны и логичны.
За подробными доказательствами и комментариями можно обратиться к литературе или
проверить эти выкладки самостоятельно с использованием таблиц истинности.
Преобразование и упрощение
логических выражений.
В начало
Как уже
говорилось выше использование законов логики позволяет равносильно
преобразовывать логические выражения, что зачастую приводит к их упрощению.
1. А V (┐А & В) = (A V ┐А) &
(AV B) = 1 & (AV B) = (1 &A) V (1 &B)
= A V B
- Выполняем дизъюнкцию с каждым из высказываний в скобках.
- Дизъюнкция A с
инверсией дает истину (1).
- Выполняем конъюнкцию с каждым из высказываний в скобках.
- Результатом конъюнкции высказывания с истиной является само
высказывание.
2. (А V В) & (┐A V B) & (С V┐B ) = B & (С V┐B ) = (B&С) V (B &┐B) = (B&┐С) V 0 =
(B V 0) & (C V 0) = B & C
- Согласно распределительному закону выводим B
за скобку из первой и второй дизъюнкций.
- Конъюнкция высказывания A
с его инверсией дают ложь.
- Дизъюнкция высказывания с ложью дает само высказывание.
- Выполняем конъюнкцию B с
каждым из высказываний в скобках.
- Конъюнкция B со своей
инверсией дают ложь.
- Дизъюнкция высказываний B и
C с ложью дают оригинальные
высказывания.
3. ┐((A v B) → ┐(B v C))
= A v B & ┐ ┐(B v C) = (A v B) & (B v C) = B v (A & C)
- Выполняем преобразование импликации согласно закону
де Моргана
- Двойная инверсия
пропадает, а высказывание
B,
согласно распределительного закона выводим за скобку.
Решение логических задач.
В начало
Логические задачи могут быть решены следующими
способами.
1. С помощью рассуждений.
2. С помощью преобразований логических выражений.
3. Табличным способом.
Рассмотрим классическую задачу с разбитой вазой.
На звук разбившейся вазы
прибежала мама. На вопрос мамы: кто это сделал, три мальчика ответили следующее.
- Саша сказал: Коля не разбивал, это Ваня.
- Вася ответил: Разбил Коля, Саша не играет в футбол.
- Коля сказал: Это не Ваня, а я еще уроки не выучил.
Как оказалось два мальчика сказали правду, а один солгал.
Метод рассуждений:
Саша: 1. Это не Коля. 2. Это Ваня.
Ваня: 1. Это Коля. 2. Это не Саша.
Коля: 1. Это не Ваня. – у Коли только одно высказывание.
Мальчиками, которые сказали правду, не могут быть одновременно Саша и Ваня, так
как их высказывания противоречат друг другу.
Это не могут быть Саша и Коля – их высказывания противоречат друг другу.
Значит, правду сказали Ваня и Коля, а Саша солгал.
Значит, вазу разбил Коля.
Метод преобразования
логических выражений.
C - вазу разбил Саша.
В – вазу разбил Ваня.
К – вазу разбил Коля.
Саша сказал: 1. ¬K 2. В
Ваня сказал: 1. К 2. ¬С
Коля сказал: 1. ¬В
Если Саша солгал, то выражение запишется: . ¬K = 0 В = 0
Если Саша сказал правду, ¬K = 1 В = 1
Рассмотрим предположения:
Коля солгал, а Саша и Ваня сказали правду.
¬K & В = 1 и К& ¬C =1 и B = 1
В результате имеем: ¬K & В & К & ¬C & B = 1
Но ¬K & К = 0 Значит ноль левой части равен единице правой.
Наше предположение неверно.
Предполагаем далее:
Ваня солгал, а Саша и Коля сказали правду.
Тогда имеем: ¬K & В = 1 и ¬K & C = 1 и ¬ В = 1
¬K & В & ¬K & C & ¬ В = 1
Учитывая что ¬B & B = 0 Левая
и правая части выражения противоречат друг другу.
Предполагаем последний вариант:
Саша солгал, а Ваня и Коля сказали правду.
K & ¬ B = 1 и K & ¬C = 1 и ¬B = 1
K & ¬ B & K & ¬C & ¬B = 1 Упростим выражение, зная, что
K & K = K ¬B & ¬B = B
K & ¬B & ¬ C = 1
Результирующее выражение указывает на то, что наше
предположение истинно и вазу разбил Коля.
Рассмотрим табличную форму
решения логических задач.
Задача.
Джуди, Айрис и Линда живут в разных городах и имеют разные профессии. Нужно
определить их профессии и местожительства если известно:
- Джуди живет не в Париже, а Линда не в Риме.
- Парижанка не снимается в кино.
- Та, что живет в Риме, певица.
- Линда равнодушна к балету.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | Джуди | 0 | ||||
| Айрис | 0 | |||||
| 0 | Линда | 0 | 0 | 1 |
Линда живет не в Риме, значит она
не певица, и равнодушна к балету, значит она актриса. А Айрис и Джуди актрисами
быть не могут.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | Джуди | 0 | ||||
| 1 | Айрис | 0 | ||||
| 0 | 0 | 1 | Линда | 0 | 0 | 1 |
Парижанка не снимается в кино,
значит Линда не парижанка, а проживает в Чикаго. Теперь мы видим, что Джуди и
Линда не живут в Париже, значит там живет Айрис.
| Париж | Рим | Чикаго | Пение | Балет | Кино | |
| 0 | 1 | Джуди | 1 | 0 | ||
| 1 | Айрис | 1 | 0 | |||
| 0 | 0 | 1 | Линда | 0 | 0 | 1 |
Теперь получается, что Джуди
живет в Риме, а значит, она певица и Айрис остается быть балериной.
Основы компьютерной микросхематики. В начало
Основой всех компьютерных устройств, построенных по цифровому принципу, являются
логические элементы.
Логический элемент это электронное устройство, выполняющее соответствующую
логическую функцию.
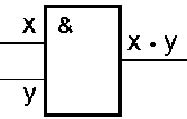
Логический элемент И
реализует конъюнкцию двух или более логических значений.
Таблица истинности схемы И
 |
X | Y | X&Y |
| 0 | 0 | 0 | |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 1 | 1 |
Логический элемент ИЛИ
реализует дизъюнкцию двух или более
логических значений.
 |
X | Y | X V Y |
| 0 | 0 | 0 | |
| 1 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 1 | 1 |
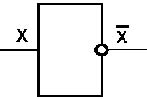
Логический элемент НЕ
реализует логическую функцию инверсия.
 |
X | Y |
| 0 | 1 | |
| 1 | 0 |
Реализация логических функций.
При помощи логических элементов в электронных
устройствах могут быть реализованы сложные логические функции. Рассмотрим
некоторые из них.
 |
F = ¬ (
X V Y)
F = ( ¬X V Y) F = ¬ ( ¬X & Y) |
 |
F = (X V Y) & ¬Y
F = (¬X & ¬Y) V Y
|
Элементы компьютерных схем.
Триггер
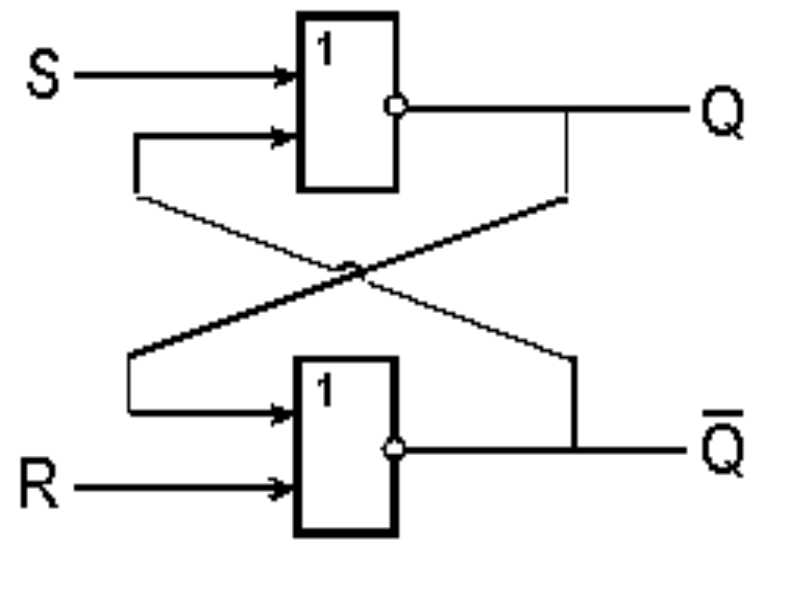 |
Триггер — это электронная схема,
предназначенная для запоминания одного разряда двоичного кода. Триггер
имеет два устойчивых состояния, одно из которых соответствует двоичной
единице, а другое — двоичному нулю. S – вход записи. R – сброс. Q – выход, хранимый бит. |
Сумматор
В целях максимального упрощения работы компьютера основная масса
математических операций сводится к сложению двоичных чисел. Поэтому главной
частью процессора является сумматор.
Сумматор — это электронно-логическая схема, выполняющая суммирование.
При сложении двоичных чисел образуется сумма в данном разряде, при этом возможен
перенос в старший разряд. Обозначим слагаемые (А, В), перенос (С) и сумму (S).
Построим таблицу сложения одноразрядных двоичных чисел с учетом переноса в
старший разряд.
|
Сложение одноразрядных двоичных чисел |
|||
|
Слагаемые |
Перенос | Сумма | |
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
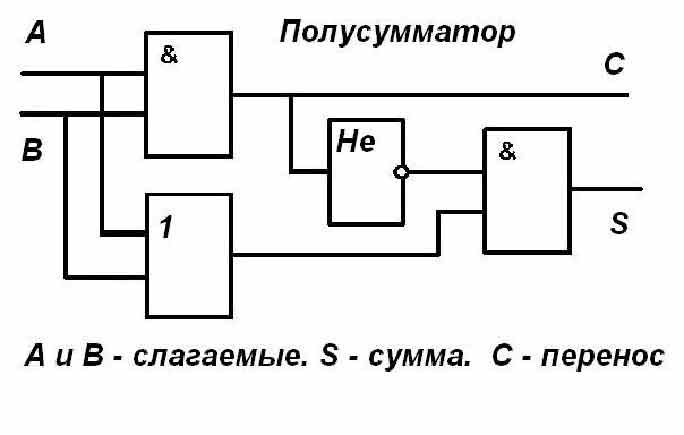 |
Данная схема называется полусумматором, так как выполняет суммирование одноразрядных двоичных чисел без учета переноса из соседнего разряда.
|
P.S. На этом заканчивается вводный курс по основам логики. Как мы видим основные положения этой науки нашли свое широкое применение в компьютерных технологиях. Поэтому для серьезного использования компьютерной техники получение прочных знаний основ логики - обязательное условие.